Cell Mechanics
In response to an inflammation in the body, leukocytes (white blood cell) interact with the endothelium (interior wall of blood vessel) through a series of steps– capture, rolling, adhesion and transmigration– critical for proper functioning of the immune system. We are numerically simulating this process using a Front-tracking finite-difference method. The viscoelastcity of the cell membrane, cytoplasm and nucleus are incorporated and allowed to change with time in response to the cell surface molecular chemistry. The molecular level forces due to specific ligand-receptor interactions are accounted for by stochastic spring-peeling model. Even though leukocyte rolling has been investigated through various models, the transitioning through subsequent steps, specifically firm adhesion and transmigration through endothelial layer, has not been modeled. We are currently modeling the transmigration process. The change of viscoelastic properties due to the leukocyte activation is observed to play a critical role in mediating the transition from rolling to transmigration.
* pic from http://bme.virginia.edu/ley/
Related Publication
-
Singh R, Li X, Sarkar K 2014 “Lateral migration of an elastic capsule in a wall-bounded shear,” Journal of Fluid Mechanics, 739, 421-443.
The migration of a capsule enclosed by an elastic membrane in a wall-bounded linearshear is investigated using a front-tracking method. A detailed comparison with themigration of a viscous drop is presented varying the capillary number (in the caseof a capsule, the elastic capillary number) and the viscosity ratio. In both cases,the deformation breaks the flow reversal symmetry and makes them migrate awayfrom the wall. They quickly go through a transient evolution to eventually reach aquasi-steady state where the dynamics becomes independent of the initial positionand only depends on the wall distance. Previous analytical theories predicted thatfor a viscous drop, in the quasi-steady state, the migration and slip velocities scaleapproximately with the square of the inverse of the drop–wall separation, whereasthe drop deformation scales as the inverse cube of the separation. These power lawrelations are shown to hold for a capsule as well. The deformation and inclinationangle of the capsule and the drop at the same wall separation show a crossoverin their variation with the capillary number: the capsule shows a steeper variationthan that of the drop for smaller capillary numbers and slower variation than thedrop for larger capillary numbers. Using the Green’s function of Stokes flow, asemi-analytic theory is presented to show that the far-field stresslet that causes themigration has two distinct contributions from the interfacial stresses and the viscosityratio, with competing effects between the two defining the dynamics. It predicts thescaling of the migration velocity with the capsule–wall separation, however, matchingwith the simulated result very well only away from the wall. A phenomenologicalcorrelation for the migration velocity as a function of elastic capillary number, walldistance and viscosity ratio is developed using the simulation results. The effects ofdifferent membrane hyperelastic constitutive equations – neo-Hookean, Evans–Skalak,and Skalak – are briefly investigated to show that the behaviour remains similar fordifferent equations.
-
Mukherjee S, Sarkar K 2014 “Lateral migration of a viscoelastic drop in a Newtonian fluid in a shear flow near a wall,” Physics of Fluids, 26, 103102.
Wall induced lateral migration of a viscoelastic (FENE-MCR) drop in a Newtonianfluid is investigated. Just like a Newtonian drop, a viscoelastic drop reaches a quasi-steady state where the lateral velocity only depends on the instantaneous distancefrom the wall. The drop migration velocity and the deformation scale inversely withthe square and the cube of the distance from the wall, respectively. The migration ve-locity varies non-monotonically with increasing viscoelasticity (increasing Deborahnumber); initially increasing and then decreasing. An analytical explanation has beengiven of the effects by computing the migration velocity as arising from an imagestresslet field due to the drop. The semi-analytical expression matches well with thesimulated migration velocity away from the wall. It contains a viscoelastic stressletcomponent apart from those arising from interfacial tension and viscosity ratio. Themigration dynamics is a result of the competition between the viscous (interfacialtension and viscosity ratio) and the viscoelastic effects. The viscoelastic stressletcontribution towards the migration velocity steadily increases. But the interfacialstresslet—arising purely from the drop shape—first increases and then decreases withrising Deborah number causing the migration velocity to be non-monotonic. The ge-ometric effect of the interfacial stresslet is caused by a corresponding nonmonotonicvariation of the drop inclination. High viscosity ratio is briefly considered to showthat the drop viscoelasticity could stabilize a drop against breakup, and the increase inmigration velocity due to viscoelasticity is larger compared to the viscosity-matchedcase.
-
Singh R, Li X, Sarkar K 2014 “Lateral migration of an elastic capsule in a wall-bounded shear,” Journal of Fluid Mechanics, 739, 421-443.
The migration of a capsule enclosed by an elastic membrane in a wall-bounded linearshear is investigated using a front-tracking method. A detailed comparison with themigration of a viscous drop is presented varying the capillary number (in the caseof a capsule, the elastic capillary number) and the viscosity ratio. In both cases,the deformation breaks the flow reversal symmetry and makes them migrate awayfrom the wall. They quickly go through a transient evolution to eventually reach aquasi-steady state where the dynamics becomes independent of the initial positionand only depends on the wall distance. Previous analytical theories predicted thatfor a viscous drop, in the quasi-steady state, the migration and slip velocities scaleapproximately with the square of the inverse of the drop–wall separation, whereasthe drop deformation scales as the inverse cube of the separation. These power lawrelations are shown to hold for a capsule as well. The deformation and inclinationangle of the capsule and the drop at the same wall separation show a crossoverin their variation with the capillary number: the capsule shows a steeper variationthan that of the drop for smaller capillary numbers and slower variation than thedrop for larger capillary numbers. Using the Green’s function of Stokes flow, asemi-analytic theory is presented to show that the far-field stresslet that causes themigration has two distinct contributions from the interfacial stresses and the viscosityratio, with competing effects between the two defining the dynamics. It predicts thescaling of the migration velocity with the capsule–wall separation, however, matchingwith the simulated result very well only away from the wall. A phenomenologicalcorrelation for the migration velocity as a function of elastic capillary number, walldistance and viscosity ratio is developed using the simulation results. The effects ofdifferent membrane hyperelastic constitutive equations – neo-Hookean, Evans–Skalak,and Skalak – are briefly investigated to show that the behaviour remains similar fordifferent equations.
-
Singh R, Li X, Sarkar K 2014 “Lateral migration of an elastic capsule in a wall-bounded shear,” Journal of Fluid Mechanics, 739, 421-443.
The migration of a capsule enclosed by an elastic membrane in a wall-bounded linearshear is investigated using a front-tracking method. A detailed comparison with themigration of a viscous drop is presented varying the capillary number (in the caseof a capsule, the elastic capillary number) and the viscosity ratio. In both cases,the deformation breaks the flow reversal symmetry and makes them migrate awayfrom the wall. They quickly go through a transient evolution to eventually reach aquasi-steady state where the dynamics becomes independent of the initial positionand only depends on the wall distance. Previous analytical theories predicted thatfor a viscous drop, in the quasi-steady state, the migration and slip velocities scaleapproximately with the square of the inverse of the drop–wall separation, whereasthe drop deformation scales as the inverse cube of the separation. These power lawrelations are shown to hold for a capsule as well. The deformation and inclinationangle of the capsule and the drop at the same wall separation show a crossoverin their variation with the capillary number: the capsule shows a steeper variationthan that of the drop for smaller capillary numbers and slower variation than thedrop for larger capillary numbers. Using the Green’s function of Stokes flow, asemi-analytic theory is presented to show that the far-field stresslet that causes themigration has two distinct contributions from the interfacial stresses and the viscosityratio, with competing effects between the two defining the dynamics. It predicts thescaling of the migration velocity with the capsule–wall separation, however, matchingwith the simulated result very well only away from the wall. A phenomenologicalcorrelation for the migration velocity as a function of elastic capillary number, walldistance and viscosity ratio is developed using the simulation results. The effects ofdifferent membrane hyperelastic constitutive equations – neo-Hookean, Evans–Skalak,and Skalak – are briefly investigated to show that the behaviour remains similar fordifferent equations.
-
Singh R, Li X, Sarkar K 2014 “Lateral migration of an elastic capsule in a wall-bounded shear,” Journal of Fluid Mechanics, 739, 421-443.
The migration of a capsule enclosed by an elastic membrane in a wall-bounded linearshear is investigated using a front-tracking method. A detailed comparison with themigration of a viscous drop is presented varying the capillary number (in the caseof a capsule, the elastic capillary number) and the viscosity ratio. In both cases,the deformation breaks the flow reversal symmetry and makes them migrate awayfrom the wall. They quickly go through a transient evolution to eventually reach aquasi-steady state where the dynamics becomes independent of the initial positionand only depends on the wall distance. Previous analytical theories predicted thatfor a viscous drop, in the quasi-steady state, the migration and slip velocities scaleapproximately with the square of the inverse of the drop–wall separation, whereasthe drop deformation scales as the inverse cube of the separation. These power lawrelations are shown to hold for a capsule as well. The deformation and inclinationangle of the capsule and the drop at the same wall separation show a crossoverin their variation with the capillary number: the capsule shows a steeper variationthan that of the drop for smaller capillary numbers and slower variation than thedrop for larger capillary numbers. Using the Green’s function of Stokes flow, asemi-analytic theory is presented to show that the far-field stresslet that causes themigration has two distinct contributions from the interfacial stresses and the viscosityratio, with competing effects between the two defining the dynamics. It predicts thescaling of the migration velocity with the capsule–wall separation, however, matchingwith the simulated result very well only away from the wall. A phenomenologicalcorrelation for the migration velocity as a function of elastic capillary number, walldistance and viscosity ratio is developed using the simulation results. The effects ofdifferent membrane hyperelastic constitutive equations – neo-Hookean, Evans–Skalak,and Skalak – are briefly investigated to show that the behaviour remains similar fordifferent equations.
-
Mukherjee S, Sarkar K 2014 “Lateral migration of a viscoelastic drop in a Newtonian fluid in a shear flow near a wall,” Physics of Fluids, 26, 103102.
Wall induced lateral migration of a viscoelastic (FENE-MCR) drop in a Newtonianfluid is investigated. Just like a Newtonian drop, a viscoelastic drop reaches a quasi-steady state where the lateral velocity only depends on the instantaneous distancefrom the wall. The drop migration velocity and the deformation scale inversely withthe square and the cube of the distance from the wall, respectively. The migration ve-locity varies non-monotonically with increasing viscoelasticity (increasing Deborahnumber); initially increasing and then decreasing. An analytical explanation has beengiven of the effects by computing the migration velocity as arising from an imagestresslet field due to the drop. The semi-analytical expression matches well with thesimulated migration velocity away from the wall. It contains a viscoelastic stressletcomponent apart from those arising from interfacial tension and viscosity ratio. Themigration dynamics is a result of the competition between the viscous (interfacialtension and viscosity ratio) and the viscoelastic effects. The viscoelastic stressletcontribution towards the migration velocity steadily increases. But the interfacialstresslet—arising purely from the drop shape—first increases and then decreases withrising Deborah number causing the migration velocity to be non-monotonic. The ge-ometric effect of the interfacial stresslet is caused by a corresponding nonmonotonicvariation of the drop inclination. High viscosity ratio is briefly considered to showthat the drop viscoelasticity could stabilize a drop against breakup, and the increase inmigration velocity due to viscoelasticity is larger compared to the viscosity-matchedcase.
-
Mukherjee S, Sarkar K 2014 “Lateral migration of a viscoelastic drop in a Newtonian fluid in a shear flow near a wall,” Physics of Fluids, 26, 103102.
Wall induced lateral migration of a viscoelastic (FENE-MCR) drop in a Newtonianfluid is investigated. Just like a Newtonian drop, a viscoelastic drop reaches a quasi-steady state where the lateral velocity only depends on the instantaneous distancefrom the wall. The drop migration velocity and the deformation scale inversely withthe square and the cube of the distance from the wall, respectively. The migration ve-locity varies non-monotonically with increasing viscoelasticity (increasing Deborahnumber); initially increasing and then decreasing. An analytical explanation has beengiven of the effects by computing the migration velocity as arising from an imagestresslet field due to the drop. The semi-analytical expression matches well with thesimulated migration velocity away from the wall. It contains a viscoelastic stressletcomponent apart from those arising from interfacial tension and viscosity ratio. Themigration dynamics is a result of the competition between the viscous (interfacialtension and viscosity ratio) and the viscoelastic effects. The viscoelastic stressletcontribution towards the migration velocity steadily increases. But the interfacialstresslet—arising purely from the drop shape—first increases and then decreases withrising Deborah number causing the migration velocity to be non-monotonic. The ge-ometric effect of the interfacial stresslet is caused by a corresponding nonmonotonicvariation of the drop inclination. High viscosity ratio is briefly considered to showthat the drop viscoelasticity could stabilize a drop against breakup, and the increase inmigration velocity due to viscoelasticity is larger compared to the viscosity-matchedcase.
-
Singh R, Li X, Sarkar K 2014 “Lateral migration of an elastic capsule in a wall-bounded shear,” Journal of Fluid Mechanics, 739, 421-443.
The migration of a capsule enclosed by an elastic membrane in a wall-bounded linearshear is investigated using a front-tracking method. A detailed comparison with themigration of a viscous drop is presented varying the capillary number (in the caseof a capsule, the elastic capillary number) and the viscosity ratio. In both cases,the deformation breaks the flow reversal symmetry and makes them migrate awayfrom the wall. They quickly go through a transient evolution to eventually reach aquasi-steady state where the dynamics becomes independent of the initial positionand only depends on the wall distance. Previous analytical theories predicted thatfor a viscous drop, in the quasi-steady state, the migration and slip velocities scaleapproximately with the square of the inverse of the drop–wall separation, whereasthe drop deformation scales as the inverse cube of the separation. These power lawrelations are shown to hold for a capsule as well. The deformation and inclinationangle of the capsule and the drop at the same wall separation show a crossoverin their variation with the capillary number: the capsule shows a steeper variationthan that of the drop for smaller capillary numbers and slower variation than thedrop for larger capillary numbers. Using the Green’s function of Stokes flow, asemi-analytic theory is presented to show that the far-field stresslet that causes themigration has two distinct contributions from the interfacial stresses and the viscosityratio, with competing effects between the two defining the dynamics. It predicts thescaling of the migration velocity with the capsule–wall separation, however, matchingwith the simulated result very well only away from the wall. A phenomenologicalcorrelation for the migration velocity as a function of elastic capillary number, walldistance and viscosity ratio is developed using the simulation results. The effects ofdifferent membrane hyperelastic constitutive equations – neo-Hookean, Evans–Skalak,and Skalak – are briefly investigated to show that the behaviour remains similar fordifferent equations.
-
Singh R, Li X, Sarkar K 2014 “Lateral migration of an elastic capsule in a wall-bounded shear,” Journal of Fluid Mechanics, 739, 421-443.
The migration of a capsule enclosed by an elastic membrane in a wall-bounded linearshear is investigated using a front-tracking method. A detailed comparison with themigration of a viscous drop is presented varying the capillary number (in the caseof a capsule, the elastic capillary number) and the viscosity ratio. In both cases,the deformation breaks the flow reversal symmetry and makes them migrate awayfrom the wall. They quickly go through a transient evolution to eventually reach aquasi-steady state where the dynamics becomes independent of the initial positionand only depends on the wall distance. Previous analytical theories predicted thatfor a viscous drop, in the quasi-steady state, the migration and slip velocities scaleapproximately with the square of the inverse of the drop–wall separation, whereasthe drop deformation scales as the inverse cube of the separation. These power lawrelations are shown to hold for a capsule as well. The deformation and inclinationangle of the capsule and the drop at the same wall separation show a crossoverin their variation with the capillary number: the capsule shows a steeper variationthan that of the drop for smaller capillary numbers and slower variation than thedrop for larger capillary numbers. Using the Green’s function of Stokes flow, asemi-analytic theory is presented to show that the far-field stresslet that causes themigration has two distinct contributions from the interfacial stresses and the viscosityratio, with competing effects between the two defining the dynamics. It predicts thescaling of the migration velocity with the capsule–wall separation, however, matchingwith the simulated result very well only away from the wall. A phenomenologicalcorrelation for the migration velocity as a function of elastic capillary number, walldistance and viscosity ratio is developed using the simulation results. The effects ofdifferent membrane hyperelastic constitutive equations – neo-Hookean, Evans–Skalak,and Skalak – are briefly investigated to show that the behaviour remains similar fordifferent equations.
-
Mukherjee S, Sarkar K 2014 “Lateral migration of a viscoelastic drop in a Newtonian fluid in a shear flow near a wall,” Physics of Fluids, 26, 103102.
Wall induced lateral migration of a viscoelastic (FENE-MCR) drop in a Newtonianfluid is investigated. Just like a Newtonian drop, a viscoelastic drop reaches a quasi-steady state where the lateral velocity only depends on the instantaneous distancefrom the wall. The drop migration velocity and the deformation scale inversely withthe square and the cube of the distance from the wall, respectively. The migration ve-locity varies non-monotonically with increasing viscoelasticity (increasing Deborahnumber); initially increasing and then decreasing. An analytical explanation has beengiven of the effects by computing the migration velocity as arising from an imagestresslet field due to the drop. The semi-analytical expression matches well with thesimulated migration velocity away from the wall. It contains a viscoelastic stressletcomponent apart from those arising from interfacial tension and viscosity ratio. Themigration dynamics is a result of the competition between the viscous (interfacialtension and viscosity ratio) and the viscoelastic effects. The viscoelastic stressletcontribution towards the migration velocity steadily increases. But the interfacialstresslet—arising purely from the drop shape—first increases and then decreases withrising Deborah number causing the migration velocity to be non-monotonic. The ge-ometric effect of the interfacial stresslet is caused by a corresponding nonmonotonicvariation of the drop inclination. High viscosity ratio is briefly considered to showthat the drop viscoelasticity could stabilize a drop against breakup, and the increase inmigration velocity due to viscoelasticity is larger compared to the viscosity-matchedcase.
Other Researches
-
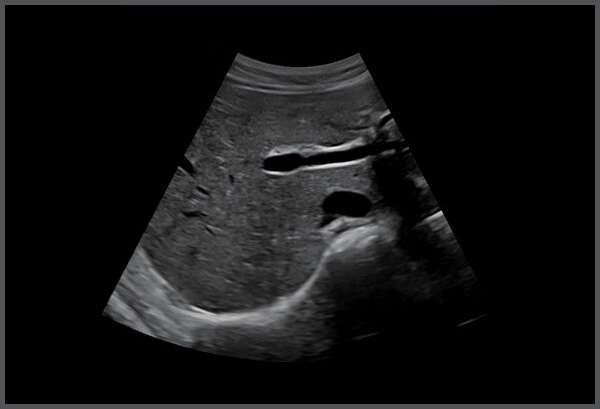
Contrast Ultrasound Imaging
Even though ultrasound remains the safest and the most popular (one in every three imaging in the world) means of imaging, its utility is limited due to poor contrast. 20% of the 17 million echocardiography performed in the United States in 2000 were suboptimal, i.e. did not provide definitive diagnosis for coronary heart disease. Microbubbles intravenously injected into patients’ body can enhance the contrast of ultrasound images. A good contrast agent will enable reliable imaging of a
-
Drug Delivery
The objective of the modern medicine is an early cost-effective accurate diagnosis of a disease, and its quick remediation with minimum side effects. Our collaborative research with Profssor Mallik of NDSU Pharmacy investigates a novel methodology using liposomes coupled with a noninvasive ultrasound mediated control and property detremination. The lipsome can contain various biomaterials such as fluorescent dyes, enzyme inhibitors, anti-cancer drugs, magnetic resonance contrast agents etc. d
-
Emulsion
Mixtures of immiscible liquids display a wide spectrum of behaviors, and thereby offer a means of achieving tunable material properties. Often they consist of small fraction of a specialized additive in a less expensive bulk liquid. The liquids phase separate into an emulsion containing discrete droplets of various sizes dispersed in a continuous phase. In industrial processing, the flow continually deforms the suspended drops leading to their coalescence and breakup. The evolving microstruct
-
Drops Bubbles
When a drop is subjected to an external flow, the balance between the interfacial tension and the flow forcing determines the drop shape while the imbalance between them leads to drop breakup. We numerically investigate deformation of a three-dimensional viscous drop forced by a potential vortex and other time-dependent extensional flows. Such flows represent oscillating forces present in multiphase flows such as due to turbulent eddies. The Simulation is performed at non-zero Reynolds number
-
Tissue Engineering